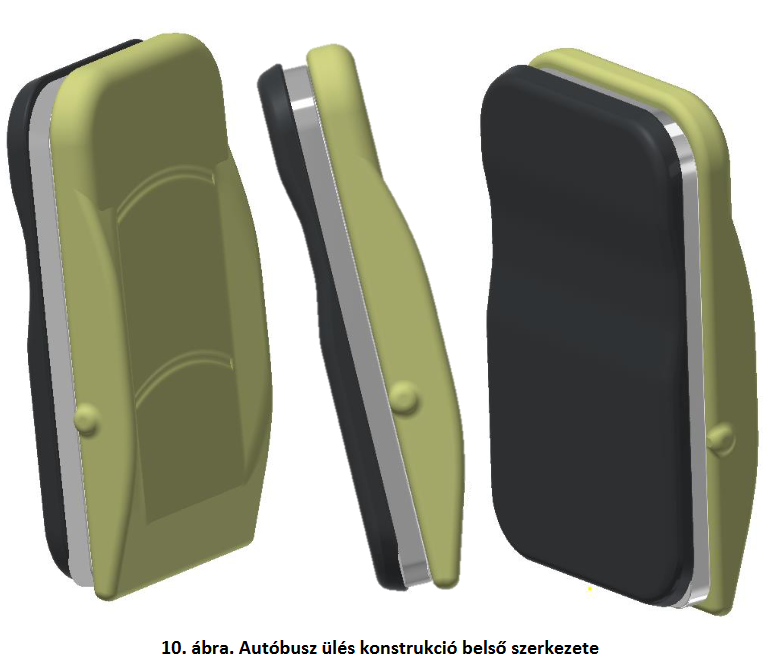
Az ülés egy több rétegű összetett, mégis egyszerűen szerelhető konstrukció. Az alábbi ábrán látható módon három eltérő rétegből épül fel.
Az ülés koncepció három rétegből tevődik össze:

A három egység egymáshoz kötelmekkel és ragasztással rögzített.
Szerelési – exploded view:
Az előző oldalon említett három egység egymáshoz rögzített. Végül kívülről egy huzat került ráhúzásra.
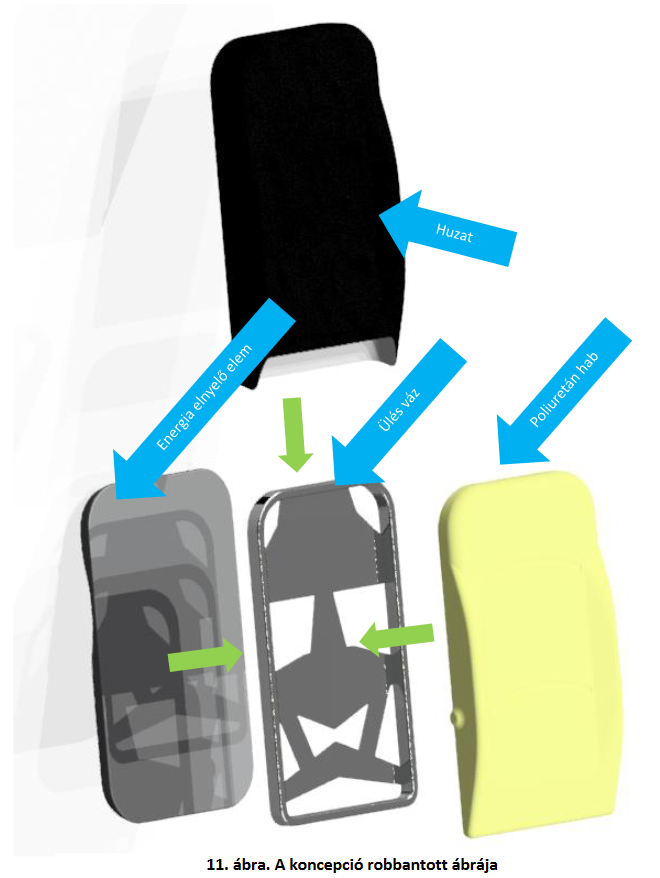
A hordágyak fejlesztési iránya a hosszirányú elmozdulás korlátozására irányult baleset esetén. Az új technológia egy olyan kiegészítő a meglévő hordágyakhoz, amely nem a leesés ellen véd (a keresztirányú szíjak ellátják ezt a funkciót), hanem a hirtelen hosszirányú lassulás (vészfékezés vagy ütközés) következményeként létrejövő lecsúszást akadályozza meg. A legbiztosabb megoldásnak a fix kialakítású ütköző felszerelése mutatkozott. A projektben négy lehetséges megoldást dolgoztunk ki és vizsgáltunk meg. A következő ábrán látható a két megvalósításra alkalmas koncepció, az eredeti számozás szerint az 1. és 4.

A két koncepció közül az elsőt javasoljuk gyártásra, mert a legkedvezőbb tulajdonságai ennek vannak. A négyes számú koncepció tartalék. A nyertes koncepció előnyei a többihez képest:
Fontosnak tartottuk a termék környezetét és az emberrel való kapcsolatát, ergonómiáját, ezért a kiindulási formám mindig egy emberi fej, majd erre a formára alakítottuk ki a védőeszköz befoglaló sziluettjét.
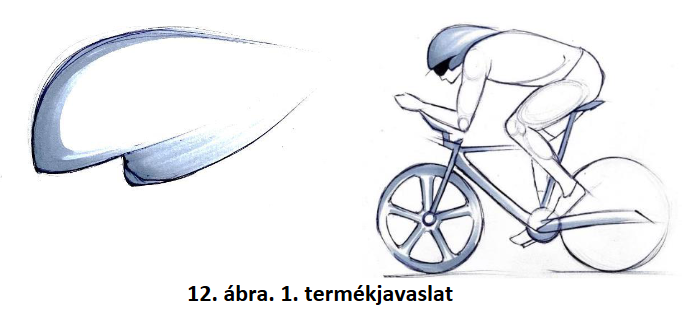
A megalkotott újszerű koncepciók megjelenésükben is egyediek, innovatívak. A termékjavaslatot a versenybiciklisek sziluettje inspirálta. Megfigyelhető, hogy a tartásuk és a kerékpárjuk kialakítása miatt a nyakrészük szinte teljesen eltűnik és a fej-vállhát részük teljesen egybefonódik.
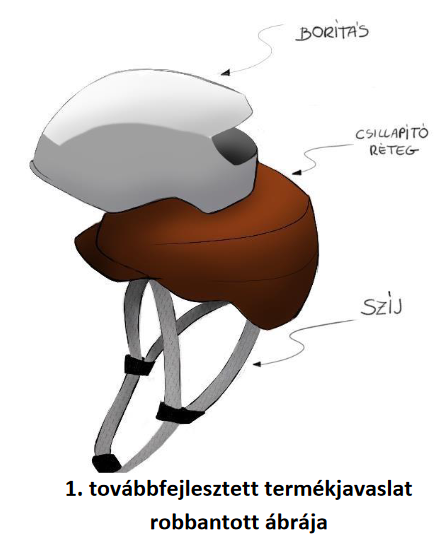
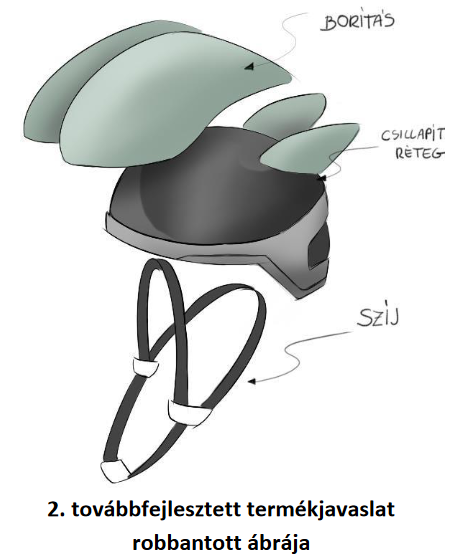
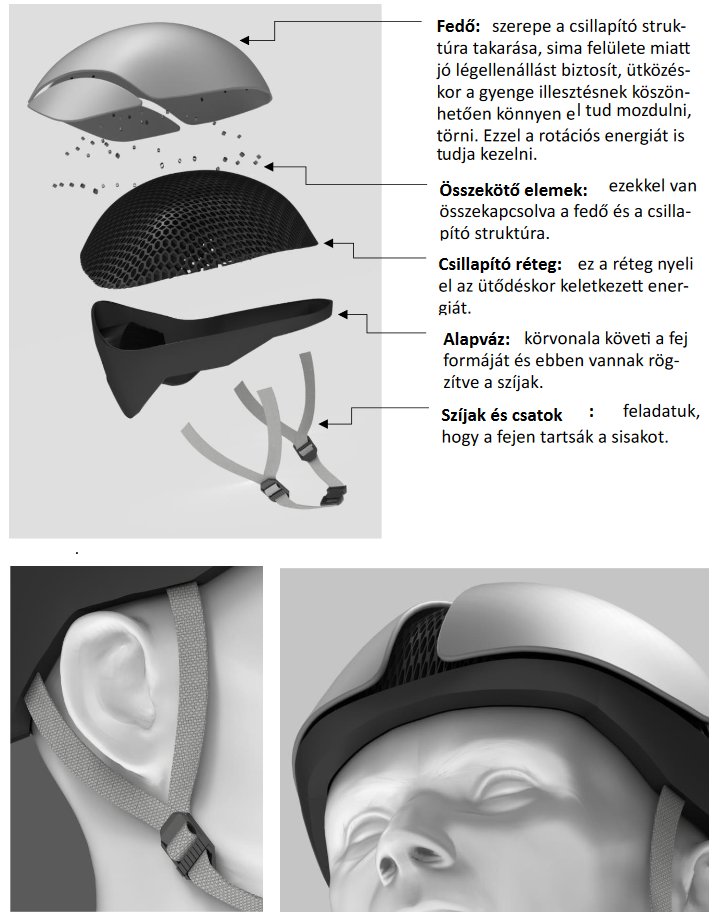
A robbantott ábrán jól látszódik milyen fő elemekből tervezzük felépíteni a bukósisakot.
A legfontosabb alkatrész a középső csillapító réteg, amely rácsszerkezetű és elég vastag a keletkező energia elnyeléséhez.
Ehhez kapcsolódik a borítás, amely a design mellett a rotációs erő csökkentésében is fontos szerepet játszik.
A mozgás jellemzők, azaz a trajektóriák becslésére különféle matematikai módszereket használunk.
A statisztikai modellek működésének lényege, hogy adott területről elegendő adat álljon rendelkezésünkre. A többi módszer esetében elegendő az elmúlt néhány másodperc adatainak rendelkezésre állnia.
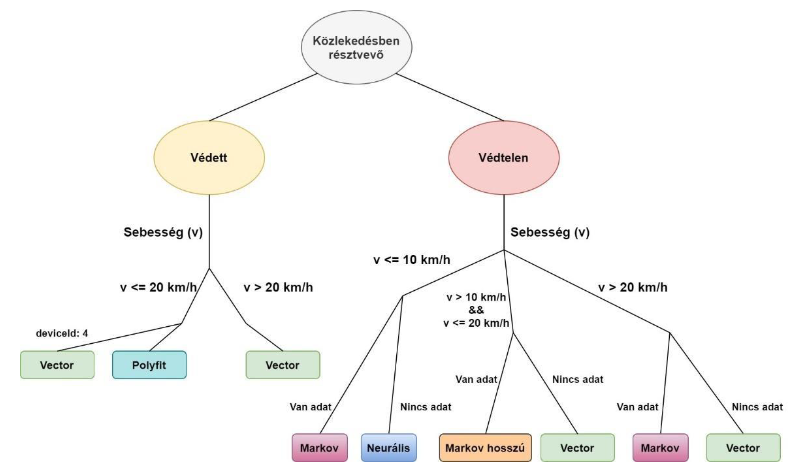
A használandó módszer kiválasztása sebesség szerinti szegmentálás alapján történik.
A Curve fit metódus egy megadott függvénynek a paramétereit keresi meg n darab próbálkozás során. Szükséges a curve fit-nek megadni egy adatsort, amire illeszteni szeretnénk a kívánt függvényünket. A függvény megpróbálja egy hibahatáron belülre rakni a paraméterezni kívánt függvényeket, mely során a legkisebb négyzetek módszerével ellenőrzi a paraméterek helyességét. Ezt a függvényt arra szokás használni, ha ismerünk egy fizikai rendszert, és tudjuk, hogy a mérni kívánt eredményeket mi befolyásolja, ezen kívül vannak mért eredményeink a rendszerről, akkor a számunkra ismeretlen paramétereket a fizikai rendszerből megpróbálja kitalálni egy bizonyos határértékkel.
Jelen esetünkben az idő függvényében a GPS koordinátákra történik az illesztés, külön a szélességi és a hosszúsági körökre. Tehát eredménynek két különböző függvényt kapjuk meg.
Predikció esetében a kapott függvényekbe behelyettesítünk jövőbeni értéket és eredményképpen megkapható a prediktált időpontban a szélességi és hosszúsági kör értékei.
A vektoros predikció az elmúlt n darab pontra illesztett vektorok átlagából számítunk jövőbeni pontok értékeit.
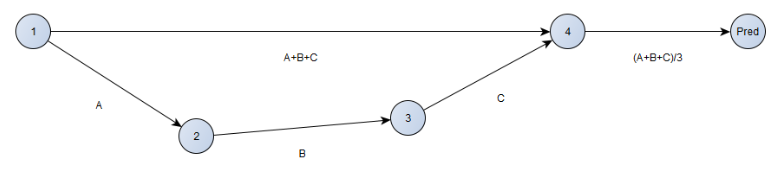
N darab pont esetén az eredményt a következőképpen számítjuk ki, ahol a v vektor a pontok
közötti vektort jelenti (fenti ábrán: A,B,C):
N-1 vektor összege:
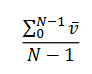
(Markov-modellek Elmélet, becslés és társadalomtudományi alkalmazások – Major Klára 2008) A Markov-láncok modelljének kulcsfogalmai az alábbiakban összegezhetők: mozgás és sokasági eloszlás. Mozgás, mivel változást, dinamikát, valamilyen átalakulást vizsgál. Ez például abban is megnyilvánul, hogy az elemzés során mindig több, különböző időpontra vonatkozó adatokat használunk és nem csak azok összehasonlítására törekszünk, de arra is, hogy az egyik időpontban megfigyelt jelenségből következtessünk a következő időpontra várható bekövetkezésre. A mozgás tehát abban is értelemben is kulcsfogalom, hogy az elemzés során törvényszerűséget keresünk, szabályt, amely magára a változásnak a magyarázatára irányul. A Markov-láncok modelljében a vizsgált objektum, amelynek időbeni változására magyarázatot keresünk, a különböző időpontokban megfigyelt sokasági eloszlás. Ezen fogalom azt írja le, hogy hogyan oszlik meg a vizsgált sokaság a vizsgálati jellemző szerint egy időpontban. Ehhez a megfigyelési egységeket különböző kategóriákba kell majd sorolnunk, ezeknek a kategóriáknak az általános neve a Markov-modell irodalmában állapot.
A kategóriák meghatározása és az egyes szóba jöhető állapotok elkülönítése a problémafelvetéstől függ: önmagában a Markov-láncok modelljének tárgyalása során teljesen érdektelen, hogy az iskolai végzettség kategóriái 0-20-ig terjedő egész számok lesznek, melyek az elvégzett évfolyamok számát mutatják, vagy képezünk öt kategóriát az előbb említett iskolai végzettségek figyelembevételével. A módszertan alkalmazásához csak az fontos, hogy a kutató eldöntse, hogy milyen kategóriákat képez. Természetesen a vizsgálati kérdés szempontjából rosszul definiált állapotok értelmezhetetlen vagy intuícióellenes kutatási eredményekhez vezethetnek, és ez így teljesen független attól, hogy magát a módszertant, a Markov-modellt, helyesen választottuk-e meg. Az alábbi ábra a Markov-modell alapfogalmai közötti sematikus kapcsolatot mutatja.
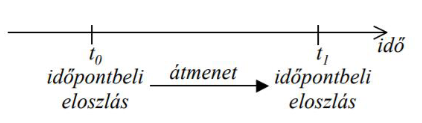
A vizsgálat a két időszakra jellemző eloszlás és a közöttük kapcsolatot teremtő átmenet szabályszerűségeinek leírására irányul. A mozgást tehát a továbbiakban átmenetnek fogjuk nevezni.
Ahhoz, hogy a modell megfelelően működjön elegendő mérési adat kell, hogy rendelkezésre álljon. A mérések során az adatok postgre sql adatbázisba kerülnek feltöltésre. A modell működésekor az aktuális pozíciónak megfelelő adatok onnan kerülnek lekérdezésre.
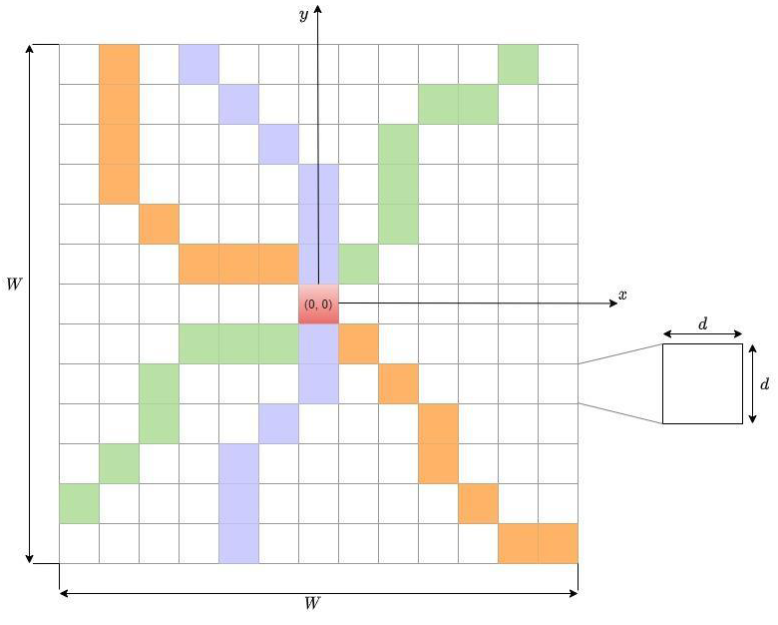
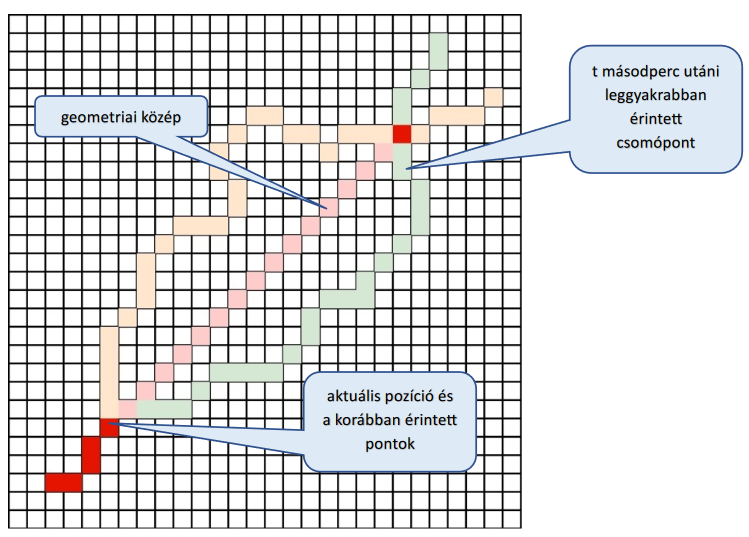
A jósláshoz egy mozgó koordinátarendszert használunk, amelynek origója a gyalogos aktuális pozíciója. Ennek megfelelően a egy rácsot hozunk létre, amelynek a sűrűsége (d), és nagysága (W) tetszőlegesen megválasztható. A predikció során összegyűjtjük az összes útvonalat, ami az origon keresztülhalad. Az ábrán ezeket az útvonalakat különböző színekkel tüntettük fel. Ezután megszámoljuk az összes egyedi útvonalat, és amelyiknek a legnagyobb gyakorisága az lesz a prediktált útvonal. A predikció során szintén paraméterezhető, hogy időben visszamenőleg hány csomópontot vegyen figyelembe, illetve, hogy hány csomópontra előre prediktáljon. Értelemszerűen minél több csomópontra szeretnék prediktálni annál pontatlanabb az eredmény. Olyan eset is előfordulhat, amikor a gyalogos pozíciója nem változik, ilyenkor ezeket ugyanúgy figyelembe veszi.
Az objektum felismeréshez mélységkamerát használunk. Az objektum felismerésért felelős kódon belül be lehet állítani, hogy mit akarunk konkrétan felismertetni vele.

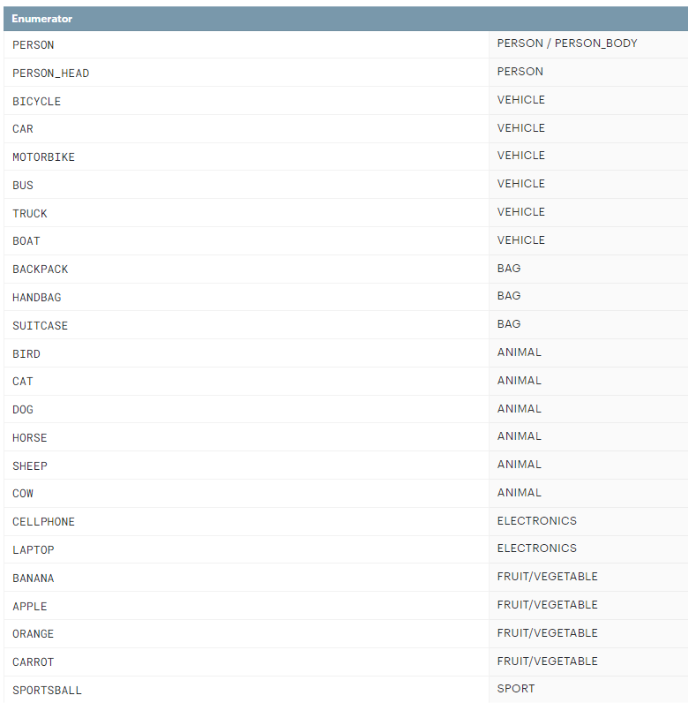
Továbbá az is beállítható, hogy a felismert objektumot 2D-s, vagy 3D-s alakzattal vegye körbe, valamint ki is írathatjuk a felismert objektum nevét.

Objektumot kétféleképpen lehet felismertetni:
Az algoritmus beolvassa a képet, majd azt egy neurális háló bemenetére kapcsolja, amely a legnagyobb valószínűségű értékkel rendelkező objektumot fogja kimenetként adni. Ezt a kimeneti értéket pedig megjelenítjük a képen: